Detekcija anomalija vremenske serije pomoću varijacionog autoenkodera (VAE)

16. 11. 2018.

Zašto detekcija anomalija vremenske serije?

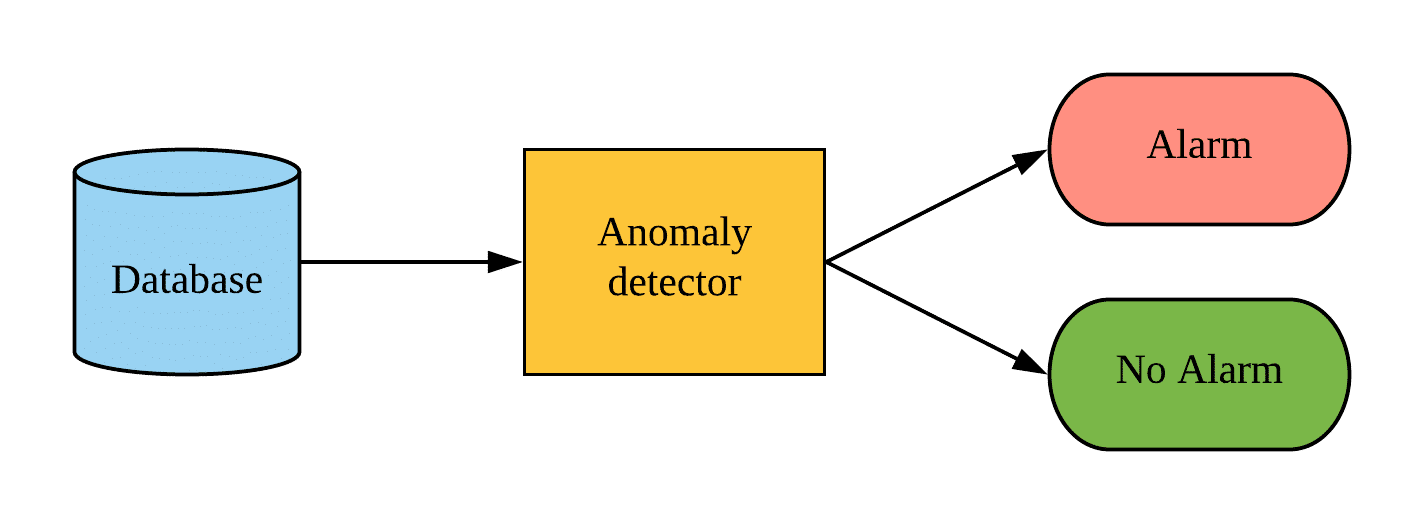
Recimo da pratite veliki broj poslovnih ili tehničkih KPI-ja (koji mogu imati sezonski karakter i šumove). U vašem je interesu da automatski izolujete vremenski okvir za jedan KPI čije ponašanje odstupa od normalnog ponašanja (kontekstualna anomalija – za definiciju pogledajte ovaj post). Kada imate problematičan vremenski okvir pri ruci, možete dalje istražiti vrednosti tog KPI-ja. Zatim možete povezati anomaliju sa događajem koji je izazvao neočekivano ponašanje. Ono što je najvažnije, tada možete delovati na osnovu informacija.

Kako bismo izvršili automatsku izolaciju vremenskog prozora, potreban nam je model mašinskog učenja za detekciju Cilj ovog posta je da predstavi probabilističku neuronsku mrežu  (VAE) kao model mašinskog učenja vremenske serije i istraži njenu upotrebu u oblasti detekcije anomalija. Kako ovaj post pokušava da smanji matematiku što je više moguće, ipak je potrebno određeno poznavanje neuronske mreže i verovatnoće.

Kontekst

Kako je Valentina pomenula u njenom postu postoje tri različita pristupa detekciji anomalija korišćenjem mašinskog učenja zasnovanog na dostupnosti oznaka:

1. nenadzirana detekcija anomalija
2. polunadzirana detekcija anomalija
3. nadzirana detekcija anomalija

Potrebno je da neko ko poznaje domen manuelno dodeli oznake. Stoga je sticanje preciznih i opsežnih oznaka dugotrajan i skup proces. Namerno sam stavio nenadziranu detekciju kao prvi pristup, jer ne zahteva oznake. Međutim, to zahteva da normalni slučajevi budu brojniji od abnormalnih. Međutim, to zahteva da normalni slučajevi budu brojniji od abnormalnih.

Koji model? Neuronske mreže stupaju na scenu…

Istorijski gledano, različite vrste neuronskih mreža su imale uspeha u modeliranju složenih nelinearnih podataka (npr. slike, zvuk i tekstualni podaci). Međutim, budući univerzalni aproksimatori funkcija kakvi jesu, oni su neizbežno našli svoj put u modeliranju tabelarnih podataka. Jedna zanimljiva vrsta tabelarnog modeliranja podataka je modeliranje vremenskih serija.

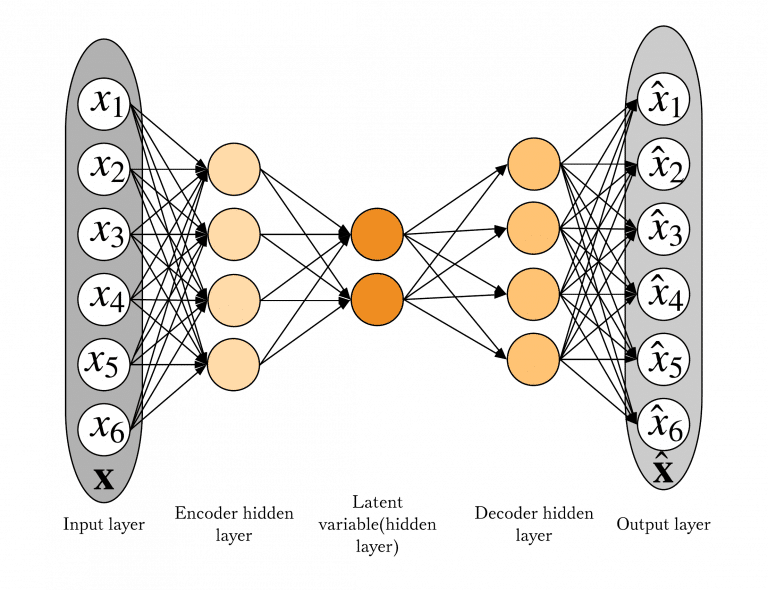
Model koji je izvršio prelazak sa složenih podataka na tabelarne podatke je Autoenkoder (AE). Autoenkoder se sastoji iz dva dela – enkodera i dekodera. Pokušava da nauči manji prikaz svog inputa (enkoder) i zatim rekonstruiše svoj input iz tog manjeg prikaza (dekoder). Ocena anomalije je dizajnirana da odgovara grešci rekonstrukcije.

Autoenkoder ima probabilističkog brata Varijacionog autoenkodera (VAE), bajesovsku neuronsku mrežu. Pokušava da ne rekonstruiše originalni input, već parametre (izabrane) distribucije izlaznih vrednosti. Ocena anomalije je dizajnirana da odgovara verovatnoći anomalije. Izbor distribucije je zadatak koji zavisi od problema, a može biti i putanja istraživanja. Sada ulazimo u malo više tehničkih detalja.

I AE i VAE koriste klizni prozor vrednosti KPI kao input. Performanse modela su uglavnom određene veličinom kliznog prozora.

Kopanje dublje u varijacione autoenkodere…

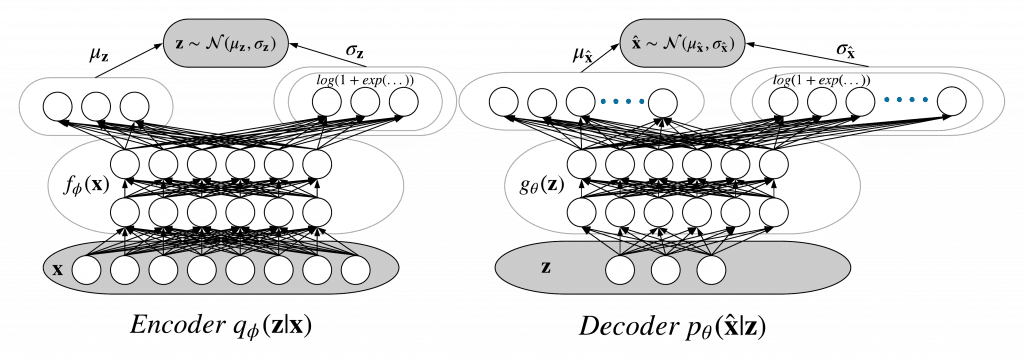
Manje zastupljenost u kontekstu VAE naziva se latentna varijabla i ima prethodnu distribuciju (odabranu da bude Normalna distribucija). Enkoder je njegova zadnja distribucija, a dekoder je njegova distribucija verovatnoće. Oba predstavljaju normalnu distribuciju u našem zadatku. Dodavanje unapred bi bilo sledeće:

1. Kodirati instancu u srednju vrednost i standardnu devijaciju latentne varijable
2. Uzorak iz distribucije latentne varijable
3. Dekodirati uzorak u srednju vrednost i standardnu devijaciju izlazne varijable
4. Uzorak iz distribucije izlazne varijable

Varijacijski autoenkoder kao probabilistička neuronska mreža (takođe nazvana Bajesova neuronska mreža). To je takođe vrsta grafičkog modela. Dubinski opis grafičkih modela može se naći u Poglavlju 8 Mašinsko učenje i prepoznavanje obrazaca Kristofera Bišopa.

Definicija modela TensorFlow:

class VAE(object):
    def __init__(self, kpi, z_dim=None, n_dim=None, hidden_layer_sz=None):
        """
        Args:
          z_dim : dimension of latent space.
          n_dim : dimension of input data.
        """
        if not z_dim or not n_dim:
            raise ValueError("You should set z_dim"
                             "(latent space) dimension and your input n_dim."
                             " \n            ")

        tf.reset_default_graph()
        
        def make_prior(code_size):
            loc = tf.zeros(code_size)
            scale = tf.ones(code_size)
            return tfd.MultivariateNormalDiag(loc, scale)

        self.z_dim = z_dim
        self.n_dim = n_dim
        self.kpi = kpi
        self.dense_size = hidden_layer_sz
        
        self.input = tf.placeholder(dtype=tf.float32,shape=[None, n_dim], name='KPI_data')
        self.batch_size = tf.placeholder(tf.int64, name="init_batch_size")

        # tf.data api
        dataset = tf.data.Dataset.from_tensor_slices(self.input).repeat() \
            .batch(self.batch_size)
        self.ite = dataset.make_initializable_iterator()
        self.x = self.ite.get_next()
        
        # Define the model.
        self.prior = make_prior(code_size=self.z_dim)
        x = tf.contrib.layers.flatten(self.x)
        x = tf.layers.dense(x, self.dense_size, tf.nn.relu)
        x = tf.layers.dense(x, self.dense_size, tf.nn.relu)
        loc = tf.layers.dense(x, self.z_dim)
        scale = tf.layers.dense(x, self.z_dim , tf.nn.softplus)
        self.posterior = tfd.MultivariateNormalDiag(loc, scale)
        self.code = self.posterior.sample()

        # Define the loss.
        x = self.code
        x = tf.layers.dense(x, self.dense_size, tf.nn.relu)
        x = tf.layers.dense(x, self.dense_size, tf.nn.relu)
        loc = tf.layers.dense(x, self.n_dim)
        scale = tf.layers.dense(x, self.n_dim , tf.nn.softplus)
        self.decoder = tfd.MultivariateNormalDiag(loc, scale)
        self.likelihood = self.decoder.log_prob(self.x)
        self.divergence = tf.contrib.distributions.kl_divergence(self.posterior, self.prior)
        self.elbo = tf.reduce_mean(self.likelihood - self.divergence)
        self._cost = -self.elbo
        
        self.saver = tf.train.Saver()
        self.sess = tf.Session()

def fit(self, Xs, learning_rate=0.001, num_epochs=10, batch_sz=200, verbose=True):
        
        self.optimize = tf.train.AdamOptimizer(learning_rate).minimize(self._cost)

        batches_per_epoch = int(np.ceil(len(Xs[0]) / batch_sz))
        print("\n")
        print("Training anomaly detector/dimensionalty reduction VAE for KPI",self.kpi)
        print("\n")
        print("There are",batches_per_epoch, "batches per epoch")
        start = timer()
        
        self.sess.run(tf.global_variables_initializer())
        
        for epoch in range(num_epochs):
            train_error = 0

            
            self.sess.run(
                self.ite.initializer,
                feed_dict={
                    self.input: Xs,
                    self.batch_size: batch_sz})

            for step in range(batches_per_epoch):
                _, loss = self.sess.run([self.optimize, self._cost])
                train_error += loss
                if step == (batches_per_epoch - 1):
                        mean_loss = train_error / batches_per_epoch   
            if verbose:
                print(
                    "Epoch {:^6} Loss {:0.5f}"  .format(
                        epoch + 1, mean_loss))
                
            if train_error == np.nan:
                return False
        end = timer()
        print("\n")
        print("Training time {:0.2f} minutes".format((end - start) / (60)))
        return True

Teorija je sjajna… Ali kako stoje stvari u stvarnom svetu?

Korišćenje modela na jednom o setova podataka iz Numenta repera anomalija (NAB):

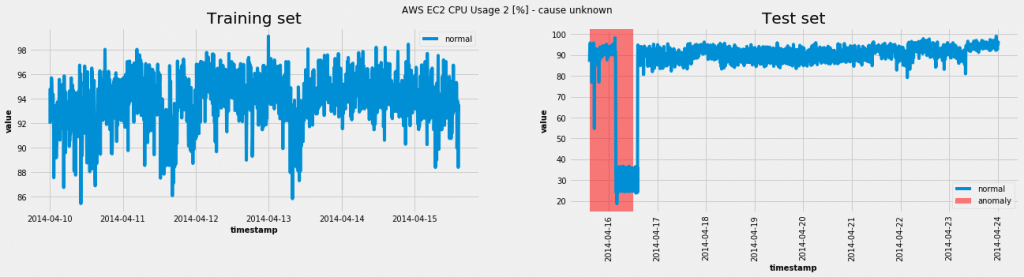
U ovom slučaju model je uspeo da postigne pravu pozitivnu stopu (TPR = 1,0) i lažnu pozitivnu stopu (FPR = 0,07). Za različte pragove verovatnoće anomalija dobijamo ROC krivu:

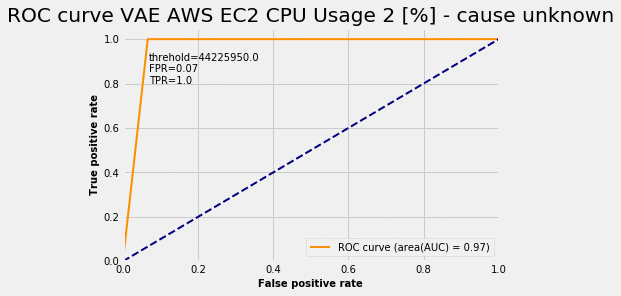
Odabirom očitanog praga sa ROC krive, dobijamo sledeće iz testnog skupa:

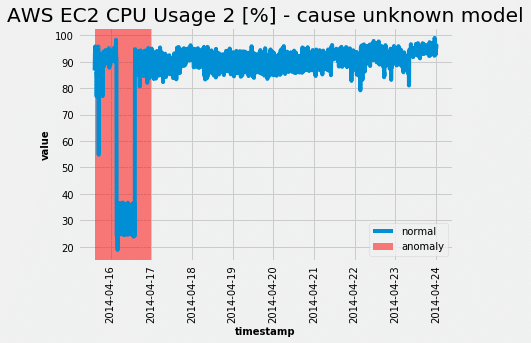
Baš kao što je ROC kriva sugerisala, model je bio u stanju da u potpunosti uhvati abnormalno ponašanje. Nažalost, pošto je svim modelima neuronskih mreža potrebno podešavanje hiperparametara, ova zver nije izuzetak. Međutim, jedini hiperparametar koji može u velikoj meri uticati na performanse je veličina kliznog prozora.

Nadam se da sam uspeo da predstavim ovaj prilično složen model jednostavnim rečima. Ohrabrujem vas da isprobate model na drugim skupovima podataka dostupnim ovde.

Nastavite sa učenjem i rešavanjem problema!