Rukovanje nedostajućim podacima

31. 08. 2017.

Zdravo svima. Iako sam planirao da moj sledeći post bude o detekciji anomalija i njihovom tretmanu, suočio sam se sa drugom vrstom problema koji je brzo prerastao u ogroman problem koji utiče na modeliranje i tačnost rezultata i nisam mogao da odolim da što pre podelim svoje iskustvo. U ovom postu ću govoriti o problemu rukovanja nedostajućim podacima.

Nedostatak podataka predstavlja svakodnevni problem za analitičara. Navikli smo se na njega i najčešće ga samo tretiramo nekim standardnim tehnikama i nastavljamo sa analizom. To je ono što sam radio dok nisam shvatio da to ne daje zadovoljavajuće rezultate.

Svi smo naučeni da je najlakši način za rukovanje nedostajućim vrednostima da ih ispustimo, naravno, ako ih nema previše. Ako postoji značajan broj nedostajućih vrednosti, neke druge opcije uključuju popunjavanje određenim vrednostima. Najzahtevniji deo ovde je odlučivanje kako treba popuniti te nedostajuće vrednosti podacima.

Pre donošenja ove odluke, važno je znati da postoje tri vrste nedostajanja podataka i nije šteta ako još niste čuli za to – moram priznati da sam to nedavno saznao.

Mogući tipovi podataka koji nedostaju su:

1. Potpuno nasumično nedostajanje (MCAR) – pojava nedostajućih vrednosti za promenljivu nije povezana sa nedostajućom vrednošću, vrednostima drugih promenljivih ili šablonom nedostajanja drugih promenljivih (sistematski nedostaci, ograničenja resursa, ograničenje režima);
2. Nasumično nedostajanje (MAR) – pojavljivanje nedostajućih vrednosti za promenljivu je nasumično, zavisno od vrednosti ili nedostatka vidljivih varijabli (odgovori sadržani u anketi, pogrešne mere, itd.);
3. Nenasumično nedostajanje (MNAR) – pojava nedostajućih vrednosti je sistematski povezana sa nepoznatim ili neizmerenim kovarijantnim faktorima (ne znamo kako se to dešava i stoga ne možemo ni na koji način da ga modeliramo).

Najvažnija stvar koju treba primetiti je da se treća vrsta nedostajanja ne može rešiti. Dobre vesti su – druge dve mogu. Dakle, ako je tip nedostatka MCAR ili MAR, ali podaci nisu modelirani, ceo proces bi rezultirao niskom efikasnošću, a u drugom slučaju – pristrasnošću. Zaključak je – trebalo bi to nekako modelirati i doći ćemo do toga. Ali prvo, hajde da navedemo tehnike tretmana.

1. Ispuštanje instanci sa nedostajućim vrednostima – kao što je gore pomenuto bi rezultiralo problemom niske efikasnosti, a možda čak i pristrasnosti u slučaju MAR. Ali pogledajmo primer u nastavku. Ova tehnika bi izbrisala obe instance, što će biti veliki gubitak informacija ako postoji mnogo instanci poput one sa ID=1.

2. Srednja imputacija – za svaku promenljivu se izračunava srednja vrednost posmatranih vrednosti i njome se popunjavaju nedostajuće vrednosti za tu promenljivu. U primeru ispod, popunili bismo nedostajuću vrednost za promenljivu w vrednosti 37, kada bi zapravo trebalo da bude 49. Ako se radi o starosti, razlika je značajna, a u praksi bi bilo još gore.

3. Imputacija zasnovana na regresiji – u ovom slučaju se pretpostavlja da se, na primer, w može izračunati kao linearna kombinacija drugih promenljivih za datu instancu, a to je sjajno ako postoji primetna korelacija između varijabli Dakle, za gornji primer može se primetiti da kada su x i y veći, vrednost w je veća, a kada su niži, vrednost w je takođe niska. Analogno, primetno je da postoji negativna korelacija između y i w. Dakle, ovde bi izračunata vrednost od 48 bila pogodnija.
4. Interpolacija podataka – koristi se uglavnom u vremenskim serijama, kada se nedostajuća vrednost može popuniti vrednošću iz prethodnog vremenskog perioda, ili prosekom dve susedne vrednosti vremenskog perioda.
5. Višestruka imputacija – u ovom slučaju, imputacija se vrši više puta, za svaku promenljivu koja nedostaje, primenom nezavisnih i zavisnih varijabli. Jedan od najčešće korišćenih algoritama sa ovakvom logikom je MICE algoritam, o čemu ćemo govoriti u nastavku.

Višestruka imputacija pomoću lančanih jednačina, poznatih kao MICE

MICE algoritam se koristi kada se suočava sa problemom MAR nedostajućih podataka – podaci koji nedostaju nasumično, ali zavise od vidljivih varijabli. Obično se sastoji od ovih koraka:

1. Imputacija srednje vrednosti – svaka vrednost koja nedostaje za određenu promenljivu se zamenjuje srednjom vrednošću za tu promenljivu;
2. U ovom koraku se bira jedna promenljiva i njene popunjene nedostajuće vrednosti se vraćaju na nultu vrednost;
3. Regresivni model se pokreće za posmatrane vrednosti promenljive iz koraka 2. U ovom regresivnom modelu, promenljiva iz drugog koraka se koristi kao zavisna, dok se (neke ili sve) druge promenljive koriste kao nezavisne;
4. Vrednosti koje nedostaju za promenljivu iz koraka 2 se zatim zamenjuju regresiranim vrednostima dobijenim primenom obučenog modela;
5. Koraci 2-4 se zatim primenjuju za svaku promenljivu u skupu podataka. Iteracija kroz svaku od ovih promenljivih čini jedan ciklus. Na kraju jednog ciklusa, sve vrednosti koje nedostaju su zamenjene predviđanjima iz regresija koje odražavaju odnose uočene u podacima;
6. Koraci 2-4 se ponavljaju tokom nekoliko ciklusa, obično deset. Očekuje se da će se koeficijenti regresije konvergirati do n-tog ciklusa, a rezultat je kompletan skup podataka.

Laka logika, i što je još važnije, došao sam do tako lepe implementacije koja dodatno olakšava korišćenje ovog algoritma. Biblioteka se naziva fancyimpute, a samu biblioteku i dokumente možete naći ovde. Kao i obično, neću vas mnogo gnjaviti sa kodom, možete ga pronaći na linku, i to je zaista svega dva reda koda.

Testirao sam ovu biblioteku na dva načina. Prvo sam je pokrenuo za objekat čije su karakteristike bile u potpunosti ispunjene. Nasumično sam postavio neke vrednosti na nulu, a zatim pokrenuo model. Nakon ovoga, izračunao sam RMSE između imputiranih i stvarnih vrednosti, i RMSE je bio prilično zadovoljavajući.

Moj skup podataka za testiranje je izgledao ovako.

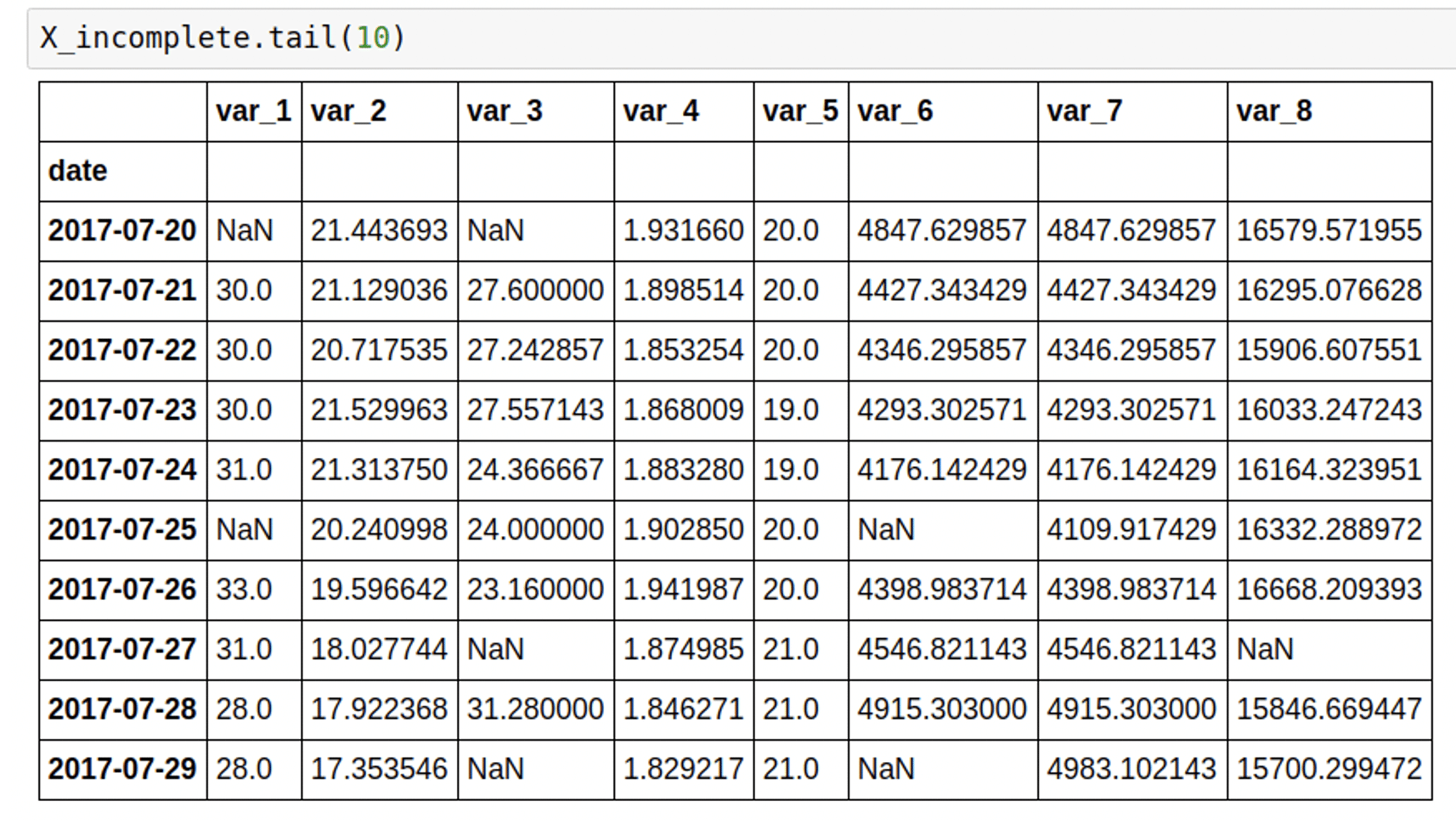
Evo koda

# import the library
from fancyimpute import  MICE

# convert dataframe to matrix, to make it workable with
X_incomplete_matrix = X_incomplete.as_matrix()

# call the function to impute the values
X_filled_mice = MICE(min_value=0).complete(X_incomplete_matrix)

# make a dataframe out of results
X_complete_with_mice = pd.DataFrame(X_filled_mice, columns = X_complete.columns)

Bilo je lako uporediti rezultate sa X_complete, koji je sadržao stvarne vrednosti. U nastavku možete videti valjanost uklapanja.

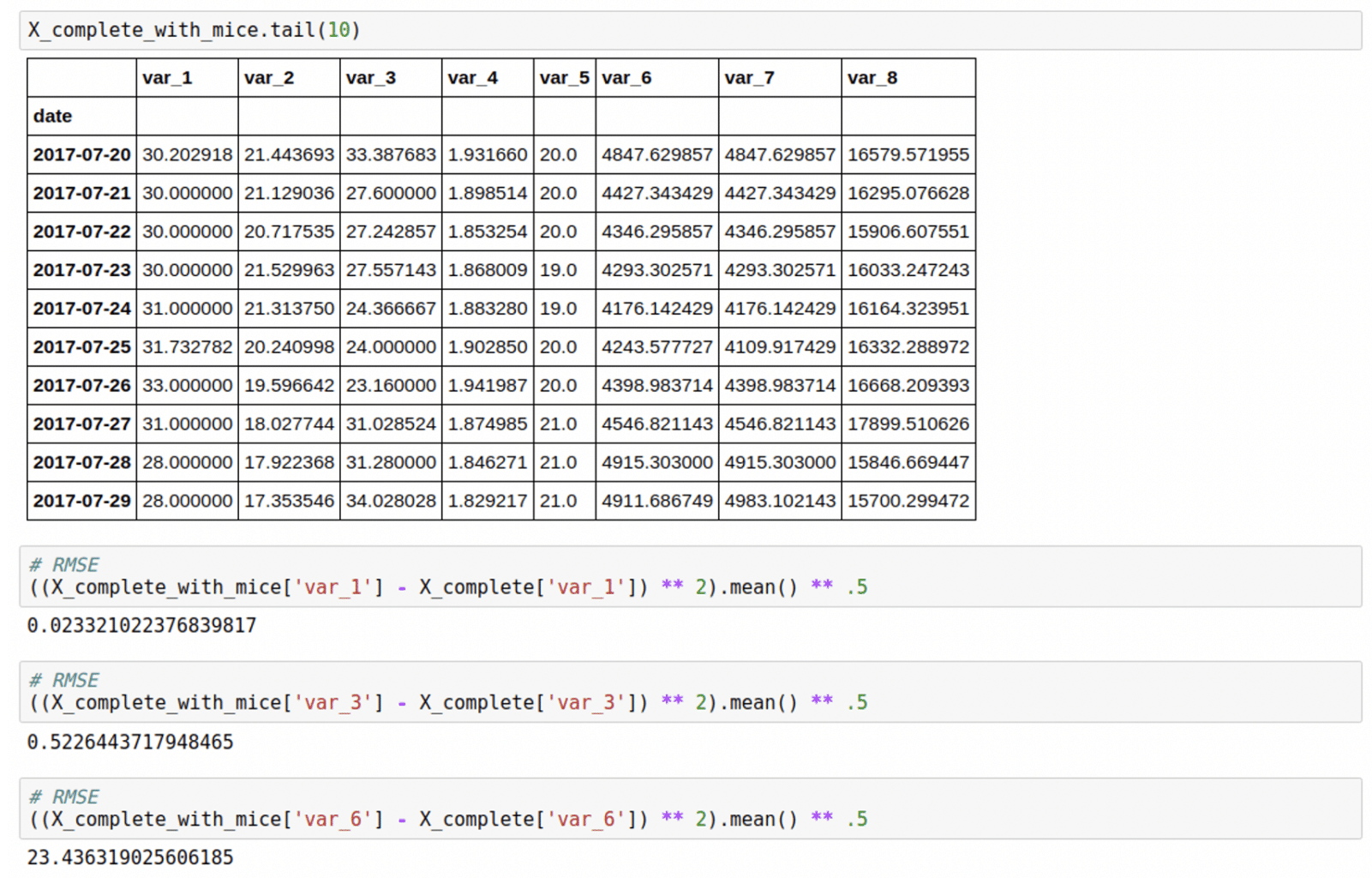
Naravno, RMSE zavisi od broja nedostajućih vrednosti, što je više nedostajućih vrednosti – veća je greška. Zato smo izveli jednu dodatnu funkciju za svaku instancu koja bi nam pomogla da radimo sa skupom podataka, tumačimo rezultate i donosimo odluke, što se naziva „pouzdanost“. Pouzdanost jednaka 100 znači da instanca ima vrednosti za sve karakteristike, i ona se smanjuje kako se broj vrednosti koje nedostaju povećava.

Drugi način validacije uključivao je konsultacije sa stručnjakom za domen i njegovu reč odobrenja. Zaključili smo da su nedostajuće vrednosti prilično precizno imputirane, tako da možemo normalno da nastavimo sa analizom.

U budućnosti ću više istraživati druge metode rukovanja nedostajućim vrednostima i ovde ću podeliti svoja iskustva. Bio bih srećan da čujem da je neko probao i ovaj, ili bilo koji drugi algoritam implementiran u gore pomenutoj biblioteci. Naravno, ako imate bilo kakvih pitanja, molim vas, ne ustručavajte se da komentarišete ispod, potrudiću se da odgovorim jasno i što je pre moguće.